From 0 to 30K - Numbers

Table of Contents
Numbers are like stars: infinite in theory, but you only see a handful at a time
Welcome to Episode 2 of the “Computer‑Science‑through‑Star Citizen” series. After dissecting latency, jitter, and bandwidth in the first post, we now turn to the foundation of every computation – how a computer actually stores numbers. Whether you’re tracking a ship’s velocity, calculating shield regeneration, or tallying in‑game credits, the underlying numeric representation dictates what’s possible, what can go wrong, and how much bandwidth you’ll burn. Mastering these basics will give you the mental toolkit for every deeper dive we’ll take later (procedural planets, AI path‑finding, network sync, you name it).
Integer Basics #
Every datum in a computer is a string of bits (0 or 1). With n bits you can encode 2ⁿ distinct values.
If you treat all n bits as unsigned, the largest value you can represent is:
| Bits | Max unsigned value |
|---|---|
| 8 | 255 |
| 16 | 65 535 |
| 32 | 4 294 967 295 |
| 64 | 18 446 744 073 709 551 615 |
In Star Citizen terms, an unsigned 32‑bit counter could theoretically track over four billion cargo units – far more than any ship could ever carry.
Most gameplay data needs to represent both positive and negative quantities (damage, velocity, score deltas, etc.). To do that we reserve one bit for the sign and use two’s‑complement for the negative range. The resulting range becomes:
| Bits | Signed range (min … max) |
|---|---|
| 8 | –128 … 127 |
| 16 | –32 768 … 32 767 |
| 32 | –2 147 483 648 … 2 147 483 647 |
| 64 | –9 223 372 036 854 775 808 … 9 223 372 036 854 775 807 |
So a signed 32‑bit integer—the type most of the game’s counters use—can hold roughly ±2 billion. That’s plenty for most in‑game values, but it is a hard ceiling; once you exceed it you get the classic overflow behaviour (the value wraps around to the opposite extreme).
Adding 1 to the largest positive signed value flips it to the most negative one1:
127 (0b01111111) + 1 → -128 (0b10000000) ← 8‑bit signed overflow
That’s why a badly‑coded cargo counter can suddenly display “‑1 ton” and make you wonder if the game has entered a black hole.
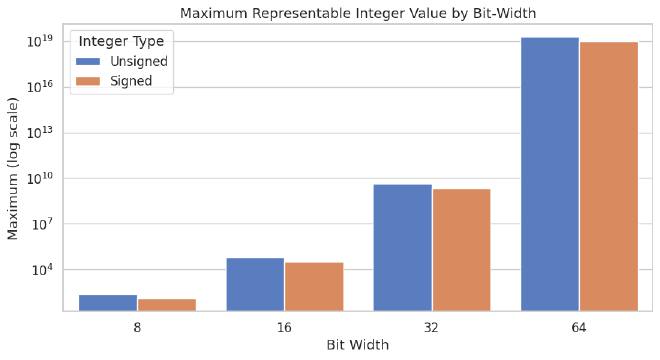
Note that the y axis in in logarithmic scale2 or the bars representing 8, 16 and 32 bits would be insignificant. This emphasizes the exponential growth of the maximum representable value as the bit‑width increases.
A quick byte primer #
In few places the article will mentions “bytes”, they are not some kind of wizardry spell, but a name to call “a group of 8 bits”.
A byte is the smallest addressable unit of memory in virtually every modern computer. When we say “a 32‑bit float occupies 4 bytes,” we mean the value is stored in a contiguous block of four bytes in RAM or in a network packet. Reducing the number of bytes per field (e.g., using a 16‑bit fixed‑point integer instead of a 32‑bit float) cuts memory usage and network traffic roughly in half.
More bits, more problems? #
It’s tempting to say, “Just switch from a 32‑bit int to a 64‑bit long and we’ll never run out of cargo slots again.” Technically that does raise the theoretical limit from ~2 billion to ~9 quintillion, which is comfortably larger than any conceivable in‑game inventory.
But the cure isn’t free:
- Memory footprint – each extra 32 bits per field means every entity that carries that field consumes four additional bytes. Multiply that by the tens of thousands of objects the server tracks (ships, missiles, debris, UI elements) and you quickly add hundreds of megabytes to the baseline memory usage.
- Network bandwidth – the server periodically streams position, health, and status packets to every client. Doubling the size of those numeric payloads roughly doubles the outbound traffic for those fields, which can push you past the comfortable margin on slower connections and increase packet loss.
- Cache pressure – modern CPUs rely on L1/L2 caches that hold only a few megabytes. Larger structures mean fewer objects fit in cache, leading to more cache misses and a measurable hit to frame‑rate, especially during dense combat scenes.
So while a long solves the finite‑range headache, it creates a new set of performance and scalability challenges that the engine must mitigate (e.g., by compressing packets, using delta‑encoding, or falling back to relative offsets).
It’s a classic engineering trade‑off: more precision → more resources.
Floating-point numbers #
Most scientific values – ship velocity, fuel consumption, laser damage – live in the realm of real numbers. Storing them exactly would require infinite bits, so we settle for the IEEE‑754 floating‑point3 formatwhich splits the bits into three logical parts:
| Part | What it stores | How it contributes to the value |
|---|---|---|
| Sign bit | 0 = positive, 1 = negative | Determines the overall sign of the number ((-1)^sign). |
| Exponent | Unsigned integer with a bias (e.g., 127 for 32‑bit, 1023 for 64‑bit) | Sets the scale: 2^(exponent − bias). Controls the magnitude (large vs. tiny numbers). |
| Mantissa | Binary fraction (23 bits for single‑precision, 52 bits for double‑precision) | Supplies the precision: the value is 1.mantissa in binary. More mantissa bits → higher precision. |
Putting it together, the numeric value is:
Intuitive picture #
Exponent → “how far left/right the decimal point moves.” Think of the exponent as deciding whether you’re dealing with a tiny micro‑meter (2⁻²⁰) or a galaxy‑scale distance (2³⁰). Changing the exponent by 1 doubles or halves the magnitude.
Mantissa → “the digits you keep after the point.” The mantissa supplies the fine‑grained detail. With 23 mantissa bits (single precision) you get about 7 decimal digits of precision; with 52 bits (double) you get about 15 decimal digits.
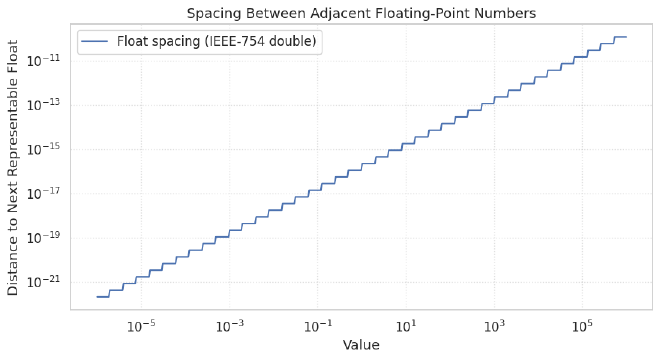
Because the exponent determines the step size, the distance between two adjacent representable numbers grows as the exponent grows. Near zero the steps are tiny (high precision); far from zero the steps become large, which is why a double can represent enormous values but loses granularity for very large numbers. This is exactly the behavior illustrated here.
Quick sanity check (Python) #
import struct
def float_bits(f):
# pack a 32‑bit float, then unpack as unsigned int to see the bits
return f'{struct.unpack(">I", struct.pack(">f", f))[0]:032b}'
print(float_bits(1.5)) # 00111111110000000000000000000000
# sign=0, exponent=01111111 (bias 127 → actual exponent 0), mantissa=100…
Reading the bit pattern confirms the three components: sign = 0 (positive), exponent = 127 → actual exponent 0, mantissa = 0.5 (the 100… part), giving (+1) × 2⁰ × (1 + 0.5) = 1.5.
Another classic demonstration: 0.1 + 0.2 does not equal 0.3 in binary floating‑point:
>>> 0.1 + 0.2
0.30000000000000004
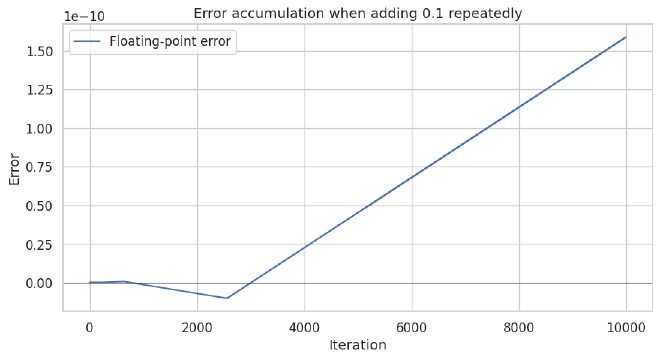
In a dogfight that extra 4 × 10⁻¹⁷ seconds can be the difference between a clean hit and a spectacular miss,
especially when the error accumulates over thousands of physics updates.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
iterations = 10000
value = 0.0
history = []
for i in range(iterations):
value += 0.1
history.append(value)
# Exact value would be i * 0.1
exact = np.arange(1, iterations+1) * 0.1
error = np.array(history) - exact
plt.figure(figsize=(9,5))
plt.plot(error, label="Floating‑point error")
plt.axhline(0, color='black', linewidth=0.5)
plt.title("Error accumulation when adding 0.1 repeatedly")
plt.xlabel("Iteration")
plt.ylabel("Error")
plt.legend()
plt.tight_layout()
plt.savefig("float_error_accum.png")
plt.show()
Fixed-point & Integer math #
Floating‑point numbers give you huge ranges, but they are non‑deterministic across CPUs and they waste memory/bandwidth (8 bytes for a double). In a massive multiplayer game like Star Citizen you often need exactly the same result on every client and you want to keep packets as small as possible. Fixed‑point solves both problems by storing a fractional value as an ordinary integer multiplied by a constant scale factor.
How it works
Pick a power‑of‑two scale (e.g., SCALE = 256, i.e. 8 fractional bits).
stored = round(real_value * SCALE) # integer stored in memory
real = stored / SCALE # convert back when you need to display
All arithmetic is then plain integer math—no hidden rounding, no platform‑dependent quirks.
Tiny Python demo (16-bit, 8-bit fraction)
SCALE = 256 # 2⁸ → each step ≈ 0.0039
def to_fixed(v): return int(round(v * SCALE))
def to_float(i): return i / SCALE
shield = to_fixed(0.45) # 45 % shield
for _ in range(5):
shield = min(shield + to_fixed(0.0075), 2**15-1) # regen @0.75 %/s
print(to_float(shield))
Output (rounded): 0.4578, 0.4657, 0.4736, 0.4815, 0.4894 – a deterministic regeneration curve that would be identical on every machine.
Benefits for game engines:
- Determinism: All clients compute the same value, eliminating desync bugs.
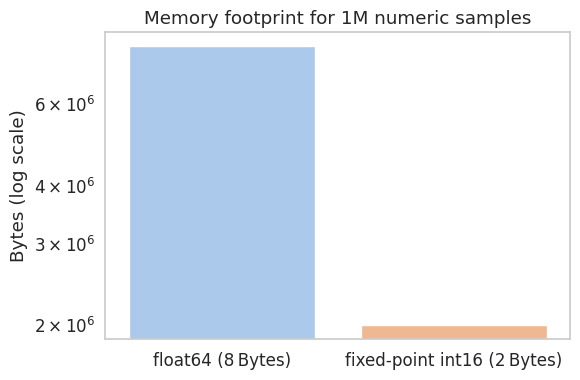
- Smaller payloads: A 16‑bit fixed‑point field (2 bytes) replaces a 32‑bit float (4 bytes), halving the bandwidth needed for things like ship velocity or fuel level.
- Cache‑friendliness: Smaller structs fit better in CPU caches, helping maintain high frame rates during crowded dogfights.
Trade‑offs:
- Limited range: With a 16‑bit signed value and SCALE = 256 you can only represent numbers up to ≈ 128. Larger ranges require a wider integer or a smaller scale.
- Quantisation: The smallest step you can represent is 1/SCALE (≈ 0.004 in the example). Very fine‑grained physics may need a finer scale, which reduces the maximum representable value.
In short, fixed‑point is the pragmatic middle ground: you keep the memory and network efficiency of integers while still being able to work with fractions—exactly what a sprawling, networked space sim needs.
Is this really the only alternative real number representation? #
Fixed‑point isn’t the only way to store real numbers—different use‑cases call for different tricks. Take in‑game currency, for instance. When you need exact currency values, a common shortcut is to store the whole‑unit part and the fractional‑cent part as two separate integers (e.g., credits = 1234, cents = 56). This avoids any floating‑point rounding quirks while keeping the representation simple and network‑friendly.
Double precision coordinates in Star Citizen #
Cloud Imperium Games has confirmed that the engine now uses 64‑bit (double‑precision) floating‑point values for world‑space coordinates4. Sean Tracy (Technical Director) explained that moving from 32‑bit to 64‑bit “allows greater precision and size for positional space”5 because the game’s star systems span millions of kilometres, far beyond what a 32‑bit float can accurately represent.
Why it matters
Precision at astronomical scales – With double precision the smallest distinguishable distance (the ulp) stays sub‑metre even when coordinates reach billions of metres, preventing the jitter you sometimes see when entering a ship.
Deterministic physics – Higher precision reduces cumulative rounding errors in trajectory calculations, essential for accurate combat, docking, and navigation across vast distances.
Performace trade-offs – Double‑precision values occupy 8 bytes each, twice the size of a 32‑bit float. That extra space means:
- Every read or write moves double the amount of data across the memory bus, which can become a bottleneck when the engine has to update millions of positions each frame.
- Because the CPU’s L1/L2 caches are limited (typically a few megabytes), larger structures mean fewer position entries fit in cache, leading to more cache‑misses and a measurable dip in frame‑rate.
- (My guess) The engine therefore reserves double‑precision only for the global world‑space coordinates that need astronomical range and sub‑metre precision. For anything that the player actually sees on screen—nearby ships, terrain patches, UI elements—it falls back to 32‑bit floats, which are natively supported by GPUs and consume half the bandwidth. As Sean Tracy explains:
GPUs themselves generally don’t work in 64‑bit – they work in 32‑bit – but the visible range stays inside 32‑bits while the overall system space is much bigger.
In short, the engine balances precision against performance by using doubles where the sheer size of the universe demands it, and floats where speed and bandwidth matter most.
So what have learned this week? #
- Integers are finite. Don’t assume you can count arbitrarily many trolleys; you’ll hit the 2³¹‑1 ceiling sooner or later.
- Floats give range, not exactness. Expect gaps that widen as numbers grow – the “real‑world” you simulate is always a bit fuzzy.
- Overflow and rounding aren’t bugs; they’re physics. They explain why a perfectly timed jump sometimes lands you inside an asteroid.
- Fixed‑point can be your friend when you need deterministic, low‑memory math (think server‑side state sync).
- Double‑precision coordinates let the universe be big but come with memory and bandwidth costs that the engine must manage.
So next time you stare at a UI element that says “Fuel: 99.999 %”, remember: the computer is guessing that last fraction, and the guess might be off by a hair. In the unforgiving vacuum of space, that hair can be the difference between a clean landing and a spectacular crash‑landing into a rock‑filled nebula.
Happy coding, and may your bits never overflow—unless you enjoy watching your cargo counter roll over into negative infinity. 🚀